В этой статье обсуждаются моды распространения света в свободном пространстве, в прозрачной однородной среде, в волноводе и в оптическом резонаторе. В качестве альтернативы, термин «мода» может также означать режим работы, т.е. синхронизация режима непрерывной волны, переключение добротности или работа на одной частоте; такую информацию см. в статье о режимах работы лазера.
Когда какой-либо световой пучок распространяется в свободном пространстве или в прозрачной однородной среде, его поперечный профиль интенсивности обычно изменяется при распространении (см. рис. 1). Однако существуют определенные распределения электрического поля, которые являются самосогласованными во время распространения, их называют «модами». Что означает «самосогласованный» в упомянутом определении, зависит от ситуации. Различные ситуации обсуждаются в следующих разделах.
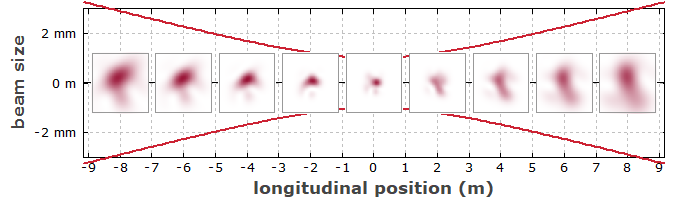
Моды в свободном пространстве
Плоские волны
Математически простейшими модами в свободном пространстве (или в оптически однородной среде) являются плоские волны. Плоская волна удовлетворяет волновому уравнению, если только произведение длины волны на оптическую частоту соответствует фазовой скорости света в среде. При распространении плоская волна меняет фазу своих колебаний и, возможно, амплитуду только в том случае, если в среде есть оптические потери или усиления.
Для данной оптической частоты и данной оптической среды волновое число k плоской волны фиксировано, но все еще возможны различные направления распространения. За математическую основу можно взять континуум плоских волн с разными направлениями распространения, а это означает, что произвольное монохроматическое распределение поля можно рассматривать как суперпозицию плоских волн. Для вычисления таких суперпозиций можно использовать преобразования Фурье. Поскольку плоские волны являются модами свободного пространства, они удобны для расчета распространения поля; это основа оптики Фурье.
Моды Гаусса, Эрмита-Гаусса и Лагерра-Гаусса
Хотя плоские волны математически очень просты, они не могут быть похожи ни на одну волну, встречающуюся в действительности, поскольку имеют бесконечную поперечную протяженность. Поэтому другие виды мод, ограниченные в поперечном пространственном измерении, часто представляют больший интерес. Простейшим видом таких мод являются гауссовы моды. Гауссовский луч расширяется или сжимается во время распространения, но является самосогласованным в том смысле, что профиль амплитуды масштабируется только в поперечном измерении, но имеет постоянную (в данном случае гауссову) форму.
Каждая гауссова мода является лишь простейшим членом целого семейства мод, которое содержит бесконечное число мод. Наиболее часто используемые семейства мод (системы мод) — это моды Эрмита–Гаусса и моды Лагерра–Гаусса. В таком семействе мод гауссова мода является основной модой, в то время как все остальные моды называются модами более высокого порядка и имеют более сложные профили интенсивности (см. рис. 2). Во время распространения поперечная протяженность каждой моды более высокого порядка изменяется пропорционально протяженности основной моды.

Обратите внимание, что для каждой комбинации оптической частоты, оси луча, положения фокуса и некоторого радиуса луча гауссовой моды в фокусе возникает целое семейство мод, например Эрмита–Гаусса.
Волноводные моды
Волноводные структуры представляют собой пространственно неоднородные структуры, которые могут направлять волны. Для света, распространяющегося в волноводе, условие самосогласования для моды более строгое, чем для мод в свободном пространстве: форма профиля комплексной амплитуды в поперечных размерах должна оставаться точно постоянной: никакое перемасштабирование не допускается, только общее изменение фазы и потеря или усиление полной оптической мощности, которые описываются постоянной распространения.
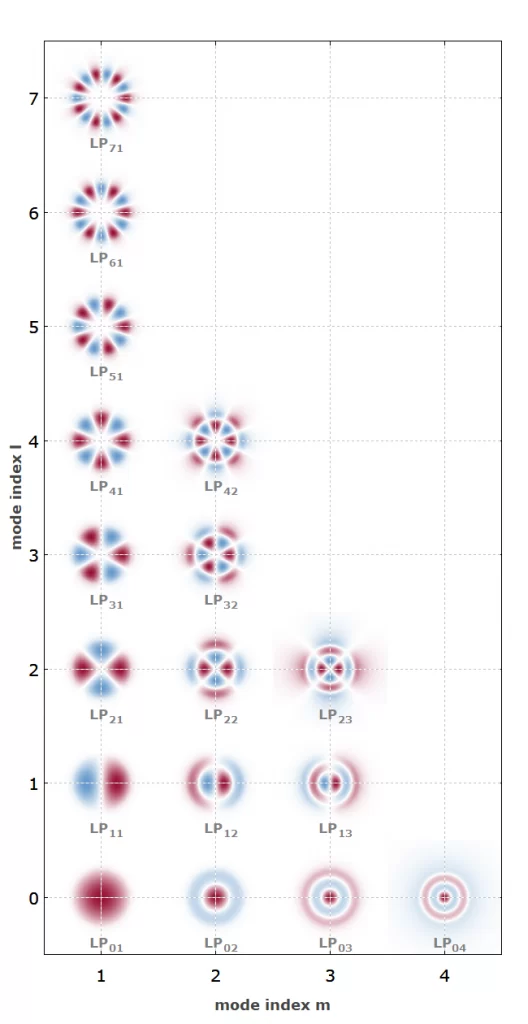
Для данной оптической частоты волновод имеет только конечное число управляемых мод распространения, распределение интенсивности которых имеет конечную протяженность вокруг сердцевины волновода. Количество направляемых мод, их поперечные амплитудные профили и их постоянные распространения зависят от деталей конструкции волновода и оптической частоты. Одномодовый волновод (например, одномодовое волокно) имеет только одну направленную моду для каждого направления поляризации. В качестве примера многомодового волновода на рис. 3 показаны поперечные профили всех мод LP многомодового волокна.
Волновод также имеет оболочечные моды, распределения интенсивности которых практически заполняют всю область оболочки (и сердцевины). Оптические волокна (даже одномодовые) имеют большое количество мод оболочки, которые часто имеют значительные потери при распространении на внешней поверхности оболочки.
Оптические волокна (за исключением фотонно-кристаллических волокон) обычно имеют радиально-симметричный профиль показателя преломления, а также относительно небольшой контраст показателей преломления между сердцевиной и оболочкой. В этом случае можно достаточно точно описать моду как моду LP, которая математически проще для описания и поэтому обычно используется на практике.
Для радиально-симметричных профилей показателя преломления также существует интересное явление мод орбитального углового момента [5, 6]. Те несут угловой момент, который не связан ни со спином фотона, ни с вращающимся направлением поляризации. Волновые фронты имеют спиральную структуру. Это возможно только для мод с нулевой интенсивностью в центре луча, например, для мод LP с ненулевым l.
Моды волокна и других волноводов можно рассчитать численно с помощью так называемых решателей мод, которые могут быть частью программного обеспечения для моделирования волокна. В зависимости от того, имеют ли волноводы радиально-симметричные профили и являются ли они слабонаправляющими, требуются алгоритмы решателя мод с разным уровнем сложности и совершенно разным временем вычислений. Решатель мод для оптических волокон, ограниченный чистыми модами LP, может быть численно намного проще и быстрее, чем обычный решатель 2D-мод.
Режимы резонатора
Для света в оптических резонаторах (из объемно-оптических элементов, а не с волноводами) условие самосогласования моды иное: мода должна воспроизвести свой точный профиль поперечной амплитуды (без перемасштабирования) только после полного прохождения резонатора — туда и обратно; во время кругового пути профиль моды может измениться по размеру и даже по форме. С другой стороны, оптическая фаза также должна быть воспроизведена после одного кругового обхода, т. е. общее наблюдаемое фазовое изменение должно быть целым числом, кратным 2π. Общая оптическая мощность может уменьшиться или увеличиться, если в резонаторе есть оптические потери или усиления.
Из-за фазового состояния моды резонатора могут существовать только для определенных оптических частот (резонансных частот). В общем, фазовый сдвиг туда и обратно зависит от картины интенсивности моды. Следовательно, разные моды более высокого порядка могут иметь разные наборы частот мод. В более простом случае геометрически стабильного резонатора существуют основные (аксиальные) моды с гауссовой формой и поперечные моды более высокого порядка, например. формы Эрмита–Гаусса. Неустойчивые резонаторы тоже имеют моды, но с гораздо более сложными модовыми свойствами.
В статье о режимах резонатора дается более подробная информация.
Применение концепции режима
Во многих фотонных устройствах свет распространяется только в одной моде. Например, одномодовый режим работы лазера означает, что возбуждается только одна мода его лазерного резонатора (т. е. несет значительную оптическую мощность). Если это действительно одна мода, а не суперпозиция нескольких осевых мод, это также подразумевает одночастотную работу. Если режим генерации является режимом Гаусса, выходной сигнал близок к дифракционно-ограниченному, т. е. имеет идеальное качество луча.
В качестве другого примера, одномодовое волокно гарантирует фиксированный профиль интенсивности на выходе, предполагая, что весь свет, запущенный в моды оболочки (неуправляемые моды), теряется до того, как будет достигнут конец волокна. Мода одномодового волокна обычно имеет форму, аналогичную гауссовой.
В других случаях часто бывает удобно разложить весь распространяющийся свет на разные моды. Это разложение означает, что для каждой моды вычисляется некоторая амплитуда моды (комплексное число, называемое вектором) для данного светового поля, обычно с использованием некоторого интеграла перекрытия. Основное преимущество такой процедуры состоит в том, что известно, как распространяются все моды: для каждой моды имеется только изменение фазы, которое можно рассчитать по ее постоянной распространения, и, возможно, некоторое изменение оптической мощности. Полная интенсивность и фазовый профиль могут быть рассчитаны для любого положения простым суммированием вкладов различных мод. Эта процедура может значительно упростить численное моделирование: большое количество амплитуд, напоминающих, например, двумерное распределение оптического поля с множеством отсчетов на мелкой сетке можно заменить относительно небольшим количеством амплитуд мод (коэффициентов возбуждения). Эта концепция, основанная на режимах, часто сильно снижает требования как с точки зрения требуемой компьютерной памяти, так и с точки зрения времени вычислений. Время вычислений, как правило, не зависит от расстояния распространения.
Концепция мод полезна, даже если условия распространения несколько отличаются от тех, для которых были рассчитаны моды. В таких случаях может происходить связывание мод: свет одной моды может быть связан с одной или несколькими другими модами. Обычно это описывается с помощью связанных дифференциальных уравнений для амплитуд мод. Такая связь мод может быть вызвана, например, нелинейными взаимодействиями при больших оптических интенсивностях или внешними возмущениями, действующими на волновод.
Библиография
| [1] | E. Snitzer, “Cylindrical dielectric waveguide modes”, J. Opt. Soc. Am. 51 (5), 491 (1961) |
| [2] | D. Gloge, “Weakly Guiding Fibers”, Appl. Opt. 10 (10), 2252 (1971) |
| [3] | A. Yariv, “Coupled-mode theory for guided-wave optics”, IEEE J. Quantum Electron. 9 (9), 919 (1973) |
| [4] | L. W. Casperson, “Mode stability of lasers and periodic optical systems”, IEEE J. Quantum Electron. 10 (9), 629 (1974) |
| [5] | L. Allen et al., “Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes”, Phys. Rev. A 45 (11), 8185 (1992) |
| [6] | M. J. Padgett, “Orbital angular momentum 25 years on”, Opt. Express 25 (10), 11265 (2017) |
| [7] | P. T. Kristensen et al., “Modeling electromagnetic resonators using quasinormal modes”, Advances in Optics and Photonics 12 (3), 612 (2020) |

